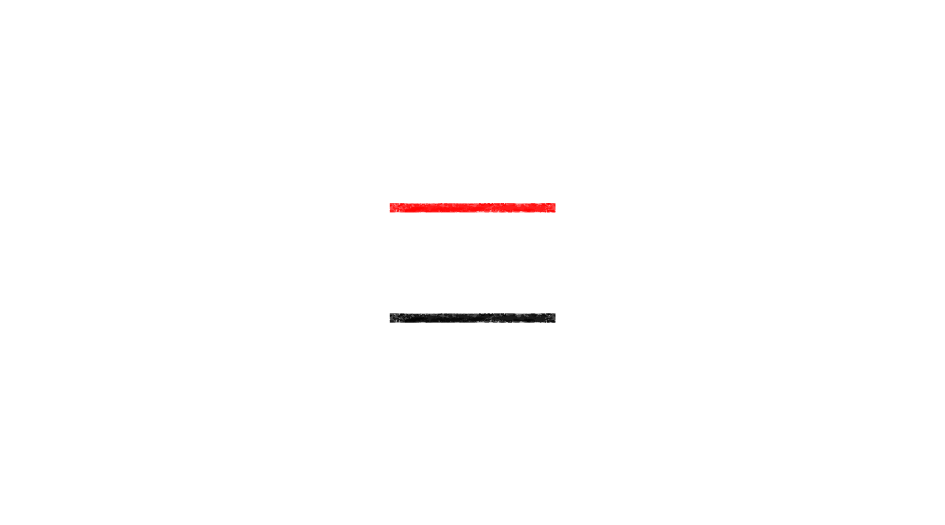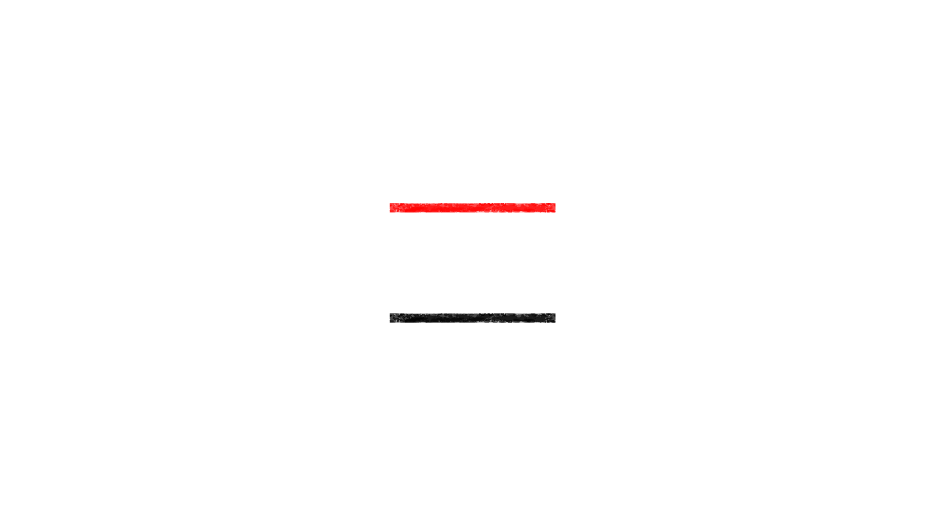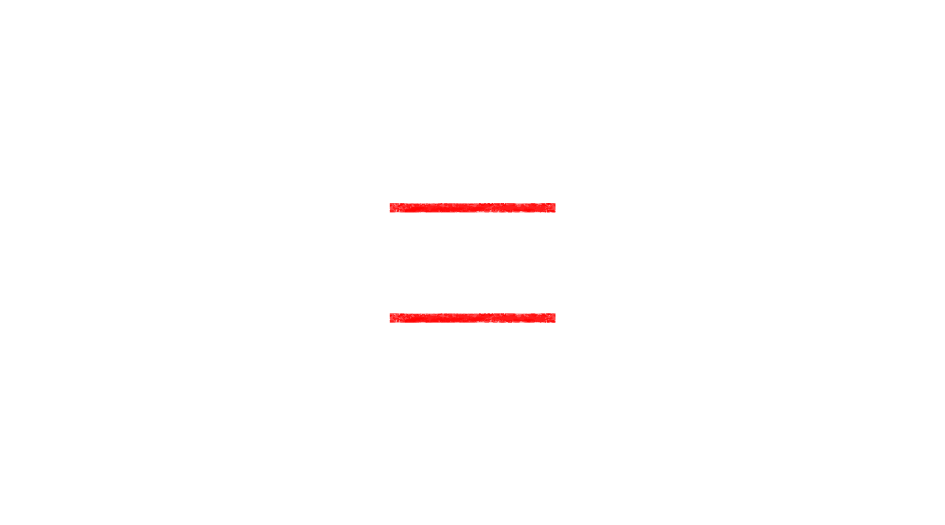ポンゾ錯視

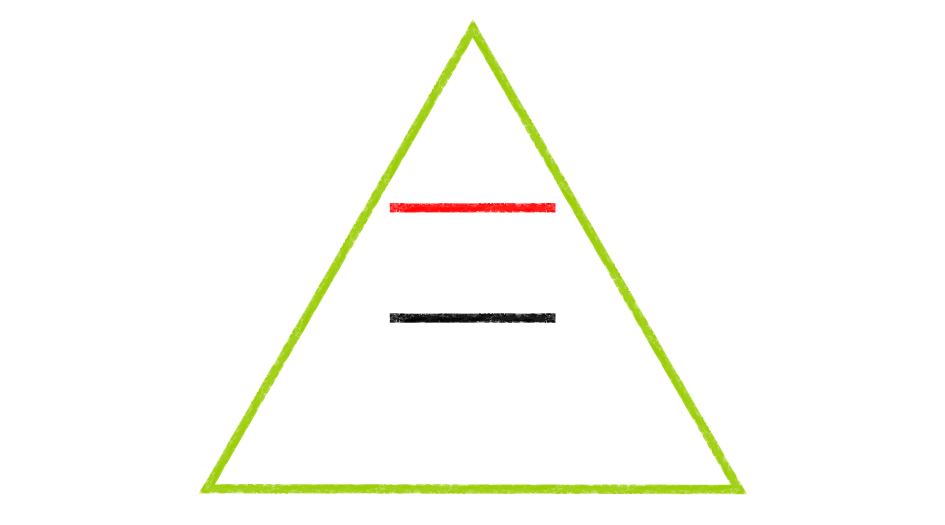
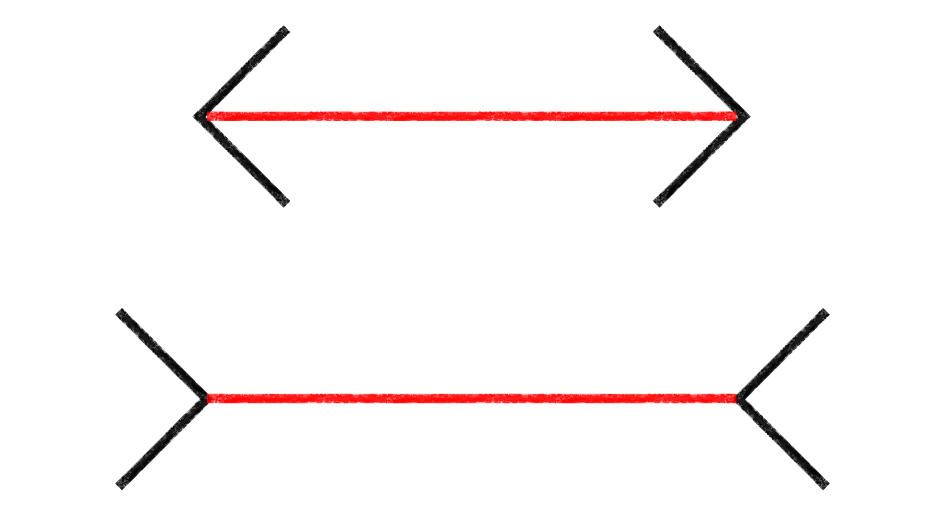
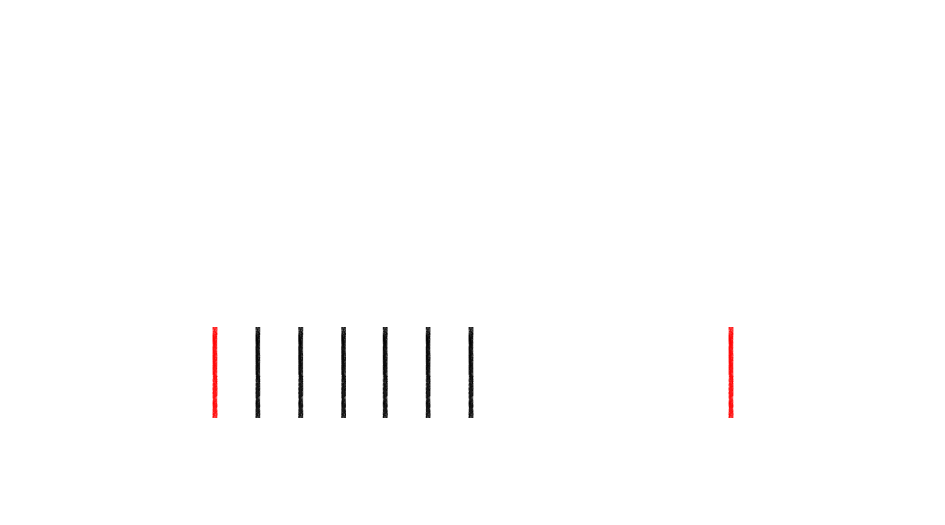
2本の線分の長さを比べてみましょう。上の赤い線の方が長く見えませんか。しかし実はどちらも同じ長さです。「すすむ」を押すか、画像を左にスワイプして、2枚目の画像に進み、周りの三角形が消えると、同じ長さであることがわかります。

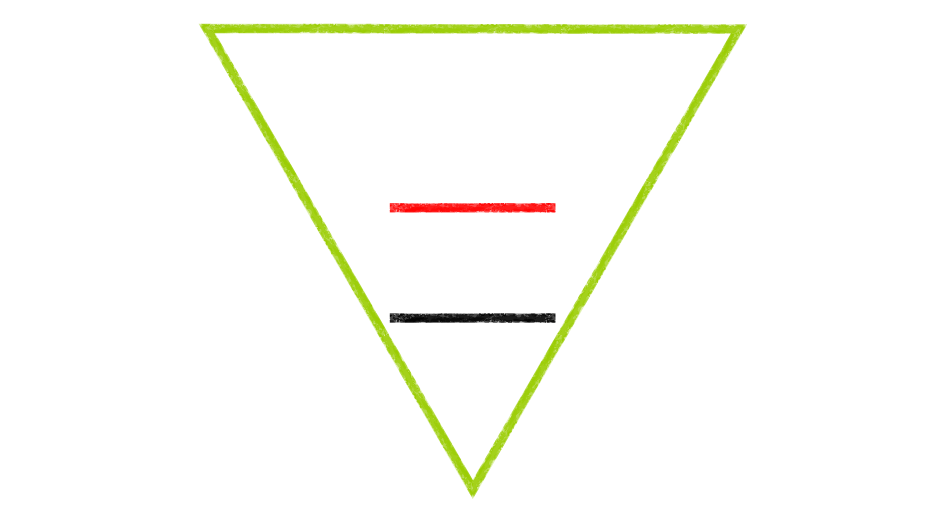
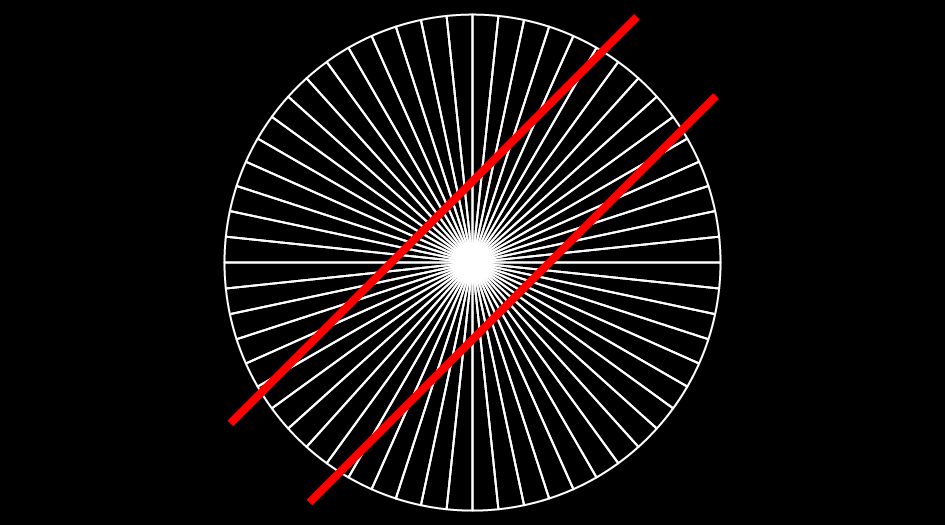
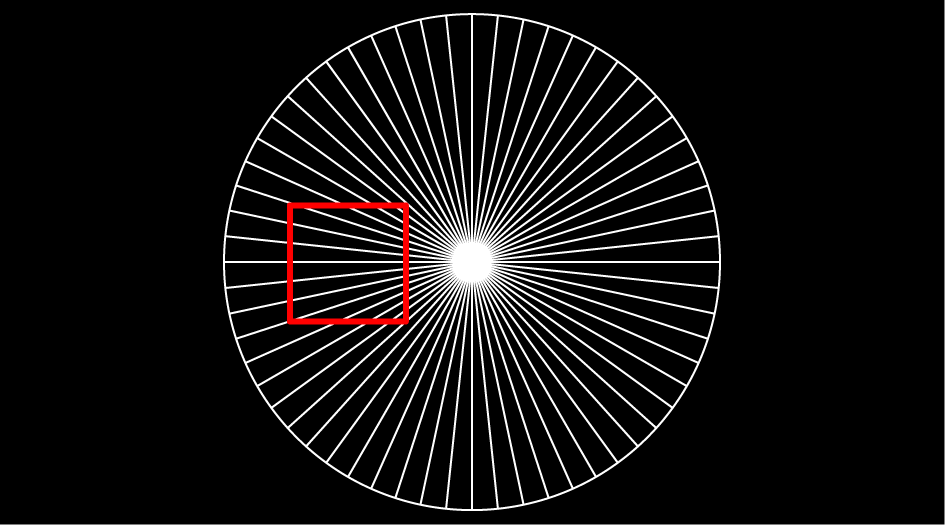
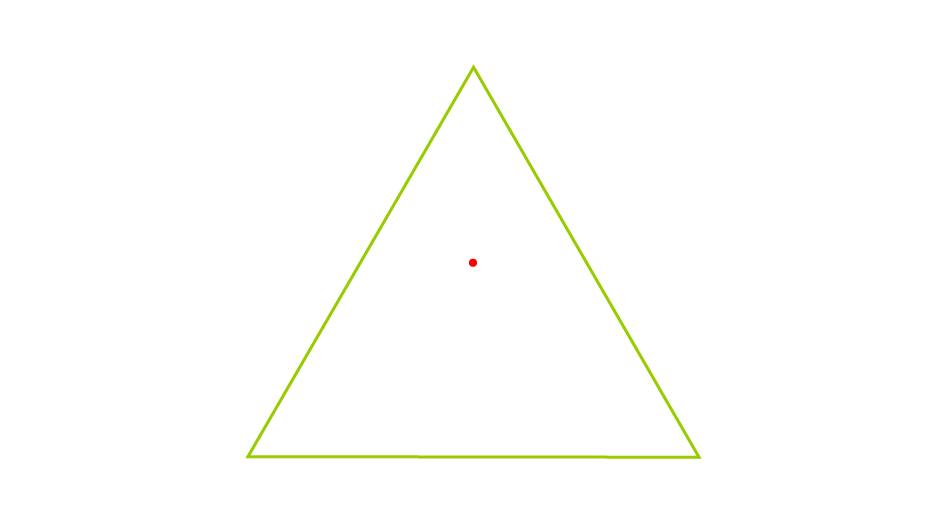
「すすむ」を押すか、画像を左にスワイプして、3枚目の画像をみてみましょう。今度は、黄緑色の三角形が反転します。このときには、線分の長さはどう見えますか？下の黒い線分のほうが少し長く見えませんか？「すすむ」を押すか、画像を左にスワイプして、4枚目の画像に進み、周りの三角形が消えると、線分の長さは同じであることがわかります。

「すすむ」を押すか、画像を左にスワイプして、5枚目の画像に進むと、線路の絵が現れます。赤い2本の線分の長さを比べると、上の方がすこし長く見えます。「すすむ」を押すか、画像を左にスワイプして、6枚目の画像に進み、背景が消えると、こちらも線分の長さは同じであることがわかります。

この錯視は、1928年にポンゾというイタリアの心理学者が考案したものです。これはしばしば遠近感にからめて説明されます。例えば三角形の2辺が、遠くへ伸びている線路だと想像してみて下さい。すると、最初の図形の場合、上が地平線の方向になります。その線路の間に置かれた2本の棒が同じ長さに見えたとしたら、実際は遠くにある方（上）が長いわけですよね。このような遠近感が錯視をひき起こしているというのです。

  奥行き情報が錯視を生じさせていることから、「ミュラーリヤー錯視」や「オービソン錯視」とも関連性があると考えられます。

参考文献

• 答えはひとつじゃない！想像力スイッチ　１．ほかの見え方はないかな？　竹内龍人・下村健一　汐文社　2020年
  （「8. 並んだ２本、どちらが長い？」でポンゾ錯視の強力なバリエーションが見られます）

デモについて

• デモの操作方法については、使用方法のページをごらんください。