説明
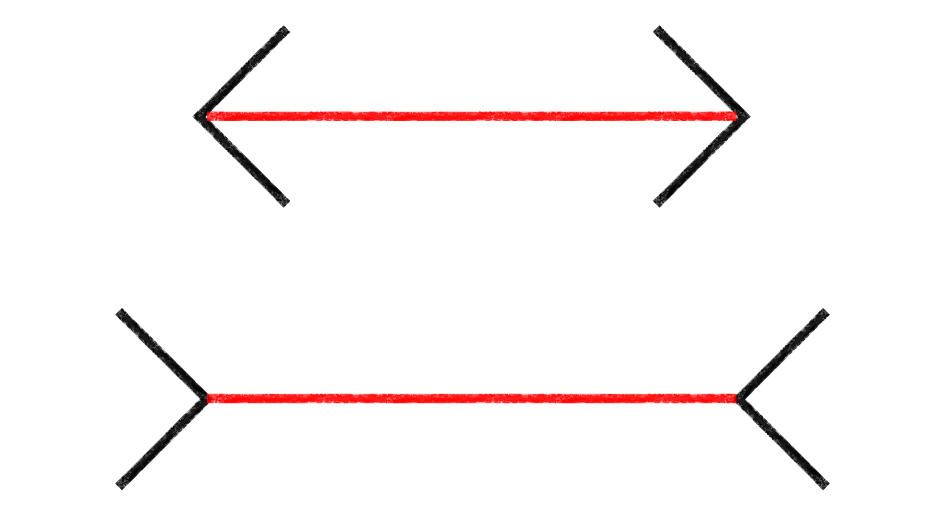
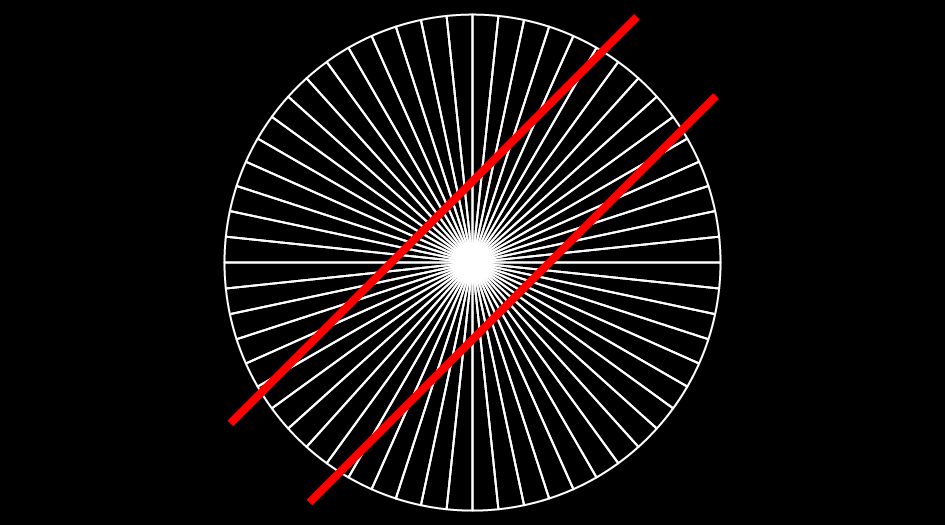
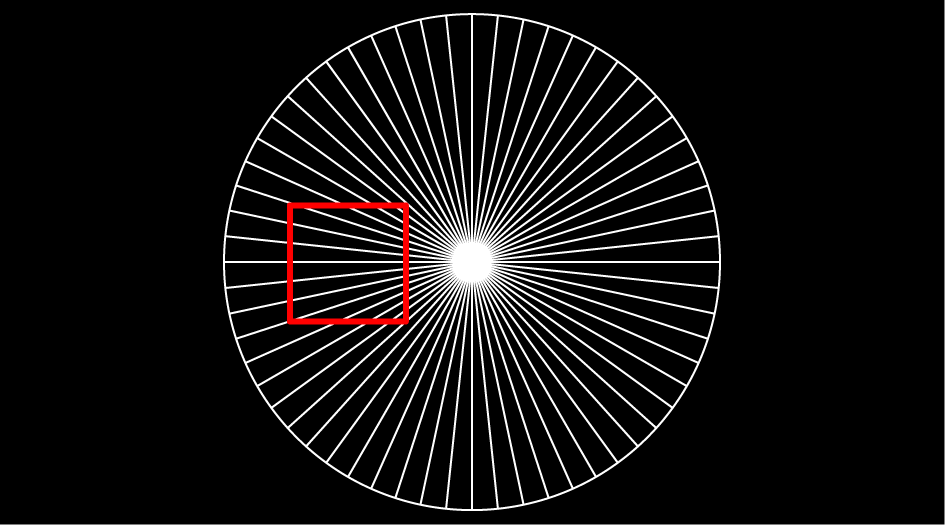
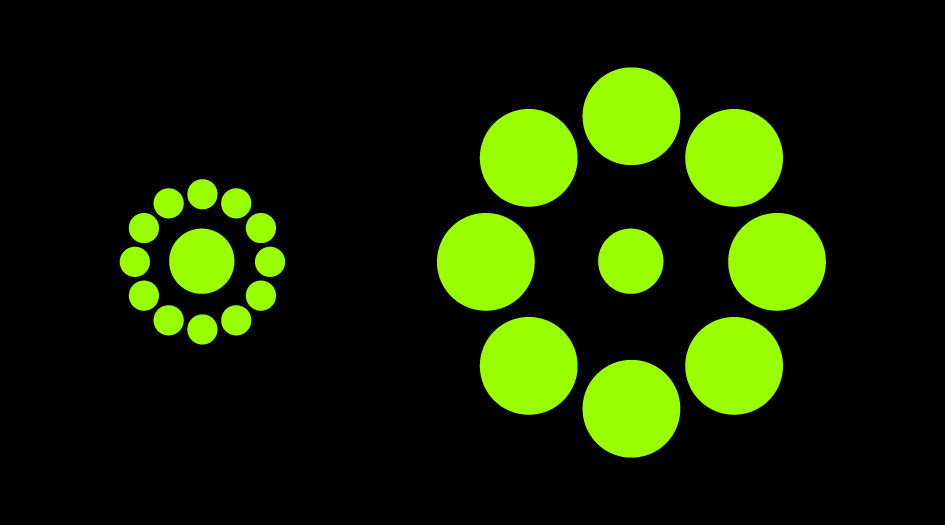
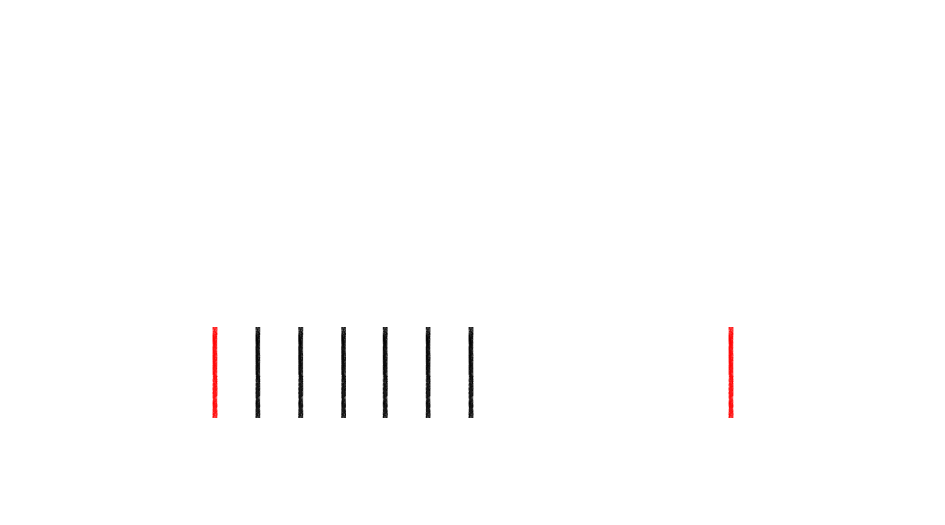
100年以上前に報告された、おなじみの錯視図形です。上下の水平線の長さを比べてください。この2本の水平線が同じ長さである、ということを知っていても、やはり下の方が長く見えます。2枚目の画像は、1枚目の画像から斜め線をとったものです。水平線から斜め線をとれば、錯視効果が消えてしまうことがわかります。
この強力な錯視はなぜ生じるのでしょうか。一つの可能性は、水平線の長さを判断するときに、視覚システムが斜め線をも含めてしまう、ということです。ミュラーリヤー図形では、斜め線と水平線は接していますから、これはありうることです。このデモでは、水平線と斜め線の色が違っています。赤い水平線の長さのみを判断しようとしても、黒い斜め線の影響を避けることはできない、ということになります。
この説明だけを聞くと、人間の目とは不正確なものだな、と思われるかもしれません。しかしながら、もう一方でまったく異なる説があります。視覚システムは不正確どころか、きわめて積極的に世界を認識しようとしている、そのしくみの表れの一つがミュラーリヤー錯視だ、というものです。
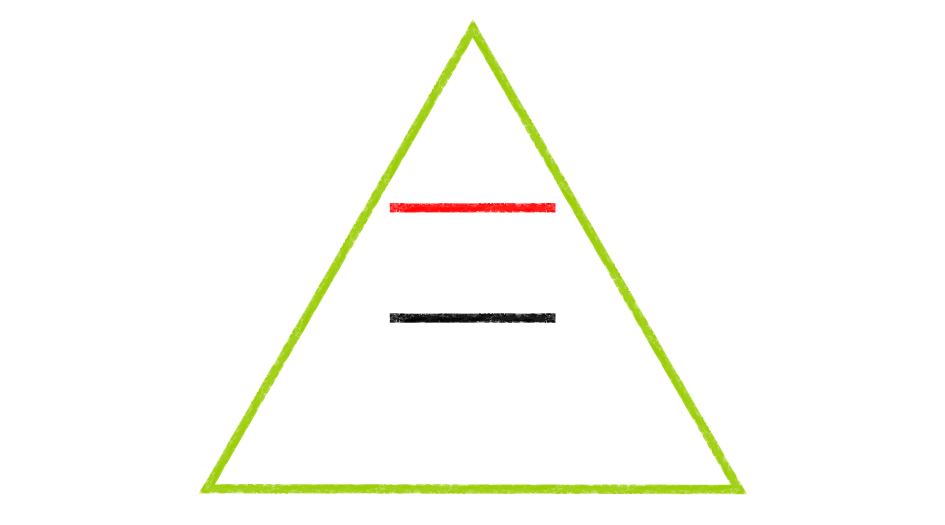
イギリスの心理学者R.グレゴリーの説によれば、ミュラーリヤー錯視には「三次元の認識」がかかわっているのです。下の図はデモのミュラーリヤー図形をタテにしたものです。短く見える方は、壁のコーナーがこちらに向かって出っ張っている様子を簡略化した絵、長く見える方は、壁のコーナーが奥に引っ込んだ様子を簡略化した絵に見えてきませんか?
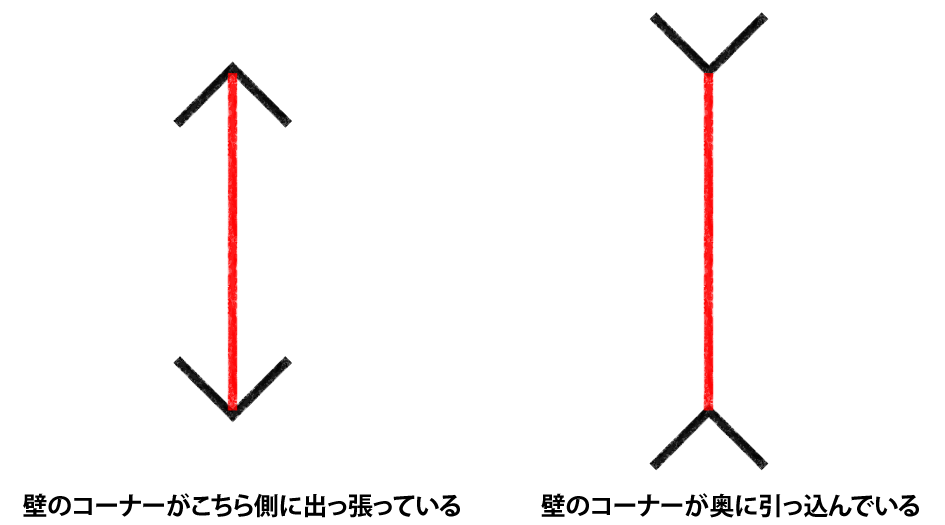
さて、視覚システムにとって、二つのコーナーにおける垂直線の物理的な長さは同じです。もうすこし詳しく説明すると、網膜(目の奥にある神経細胞群のシート)に投影された垂直線の長さは同じです。しかし、上に書いたように、脳は、線が存在する奥行きが違う、と解釈しています。つまり、右側の、コーナーが奧に引っ込んでいる垂直線の方が、左側の、コーナーが出っ張っている垂直線より、遠くにあると判断しています。視覚システムはきわめて賢いことに、「それぞれの奥行きは違うはずなのに、網膜に写っている2本の垂直線の長さは同じだ。ということは、右側の垂直線は、ずっと長いのだな」と判断し、それがミュラーリヤー錯視を生み出している、という説明です。
この仮説の重要性は、私たちの視覚システムが、たとえ二次元平面(紙やモニターの画面)に描かれたパターンであっても、それを三次元世界の中のものとして積極的に解釈している、という側面を捉えている点にあります。このような考え方は、他の多くの錯視を説明する際にもあてはまります。
しかしながら、話はまだ終わりません。ミュラーリヤー錯視に関しては、さらに興味深い仮説が提案されており、まだまだ決着がついていないのが現状です(例えば Howe & Purves, 2005)。
参考文献
- Gregory, R. L. (1997) Knowledge in perception and illusion. Phil. Trans. R. Soc. Lond. B, 352, 1121-1128.
- Howe, C. Q. & Purves, D. (2005) The Muller-Lyer illusion explained by the statistics of image-source relationships. PNAS, 102, 1234-1239.
デモについて
- デモの操作方法については、使用方法のページをごらんください。